Warum ist (a | b ) äquivalent zu a - (a & b) + b?

Question

Ich suchte nach einer Möglichkeit, BITOR() mit einer Oracle-Datenbank zu verwenden, und stieß auf den Vorschlag, stattdessen einfach BITAND() zu verwenden, wobei BITOR(a,b) durch a + b - BITAND(a,b) ersetzt wird.

Ich habe es ein paar Mal von Hand getestet und festgestellt, dass es für alle Binärzahlen, die mir einfallen, zu funktionieren scheint, aber ich kann keinen schnellen mathematischen Beweis dafür finden, warum das richtig ist.
Kann mich jemand aufklären?

Answer 1

A & B ist die Menge der Bits, die sowohl in A als auch in B eingeschaltet sind. A - (A & B) ergibt alle Bits, die nur in A eingeschaltet sind. Addiert man B dazu, erhält man alle Bits, die in A oder in B eingeschaltet sind.

Die einfache Addition von A und B funktioniert nicht, weil beide Bits eine 1 haben. Wenn wir zuerst die Bits entfernen, die A und B gemeinsam haben, wissen wir, dass (A-(A&B)) keine gemeinsamen Bits mit B hat, so dass die Addition garantiert keinen Übertrag ergibt.

Answer 2

Stellen Sie sich vor, Sie haben zwei Binärzahlen: a y b . Und nehmen wir an, dass diese Zahlen nie gleichzeitig 1 in einem Bit haben, d. h. wenn a in irgendeinem Bit eine 1 hat, wird die b hat immer 0 in dem entsprechenden Bit. Und in der anderen Richtung, wenn b in irgendeinem Bit 1 hat, dann a hat immer 0 in diesem Bit. Zum Beispiel

a = 00100011
b = 11000100

Dies wäre ein Beispiel für a y b die die obige Bedingung erfüllen. In diesem Fall ist es einfach zu sehen, dass a | b wäre genau dasselbe wie a + b .

a | b = 11100111
a + b = 11100111

Nehmen wir nun zwei Zahlen, die unsere Bedingung verletzen, d.h. zwei Zahlen haben mindestens eine 1 in einem gemeinsamen Bit

a = 00100111
b = 11000100

Ist a | b dasselbe wie a + b in diesem Fall? Nein

a | b = 11100111
a + b = 11101011

Warum sind sie unterschiedlich? Sie sind anders, denn wenn wir + das Bit, das in beiden Zahlen eine 1 hat, erzeugen wir so genannte tragen : Das resultierende Bit ist 0, und 1 wird zum nächsten Bit nach links übertragen: 1 + 1 = 10 . Betrieb | hat keinen Übertrag, also 1 | 1 ist wiederum nur 1.

Dies bedeutet, dass der Unterschied zwischen a | b y a + b tritt dann und nur dann auf, wenn die Zahlen mindestens eine 1 im gemeinsamen Bit haben. Wenn wir zwei Zahlen mit 1 in gemeinsamen Bits addieren, werden diese gemeinsamen Bits "zweimal" addiert und erzeugen einen Übertrag, der die Ähnlichkeit zwischen a | b y a + b .

Jetzt schauen Sie sich a & b . Was bedeutet a & b berechnen? a & b ergibt die Zahl, die in allen Bits eine 1 enthält, wenn beide a y b haben 1. in unserem letzten Beispiel

a =     00100111
b =     11000100
a & b = 00000100

Wie Sie oben gesehen haben, sind dies genau die Teile, die die a + b abweichen von a | b . Die 1 in a & b geben Sie alle Positionen an, an denen ein Übertrag stattfinden wird.

Wenn wir nun a - (a & b) wir effektiv entfernen (subtrahieren) alle "verletzenden" Bits von a und nur solche Bits

a - (a & b) = 00100011

Zahlen a - (a & b) y b haben keine gemeinsamen 1-Bits, was bedeutet, dass wir bei der Addition a - (a & b) y b werden wir nicht auf einen Übertrag stoßen, und wenn man darüber nachdenkt, sollten wir zu demselben Ergebnis kommen, als wenn wir einfach nur a | b

a - (a & b) + b = 11100111

Answer 3

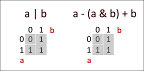
A&B = C, wobei alle Bits, die in C gesetzt sind, sowohl in A als auch in B gesetzt sind.
Entweder A-C = D oder B-C = E setzt nur diese gemeinsamen Bits auf 0. Es gibt keinen Übertragseffekt, da 1-1=0.
D+B oder E+A ist ähnlich wie A+B, mit dem Unterschied, dass durch die vorherige Subtraktion von A&B kein Übertrag entsteht, da alle gemeinsam gesetzten Bits in D oder E gelöscht wurden.

Das Endergebnis ist, dass A-A&B+B oder B-A&B+A äquivalent zu A|B ist.

Hier ist eine Wahrheitstabelle, falls das immer noch verwirrend ist:

 A | B | OR   A | B | &    A | B | -    A | B | + 
---+---+---- ---+---+---  ---+---+---  ---+---+---
 0 | 0 | 0    0 | 0 | 0    0 | 0 | 0    0 | 0 | 0  
 0 | 1 | 1    0 | 1 | 0    0 | 1 | 0-1  0 | 1 | 1
 1 | 0 | 1    1 | 0 | 0    1 | 0 | 1    1 | 0 | 1  
 1 | 1 | 1    1 | 1 | 1    1 | 1 | 0    1 | 1 | 1+1

Beachten Sie die Übertragszeilen in den + und - Operationen, die wir vermeiden, weil A-(A&B) die Fälle festlegt, in denen beide Bits in A und B 1 bis 0 in A sind, dann bringt das Zurückaddieren von B auch die anderen Fälle, in denen es eine 1 entweder in A oder B gab, aber nicht, wo beide 0 hatten, so dass die OR Wahrheitstabelle und die A-(A&B)+B Wahrheitstabelle identisch sind.

Eine andere Möglichkeit, es zu sehen, ist, dass A+B fast wie A|B ist, außer dem Übertrag in der unteren Zeile. A&B isoliert diese untere Zeile für uns, A-A&B verschiebt diese isolierten Cases in der +Tabelle um zwei Zeilen nach oben, und (A-A&B)+B wird äquivalent zu A|B.

Man könnte dies in A+B-(A&B) umwandeln, aber ich hatte Angst vor einem möglichen Überlauf, aber das war wohl ungerechtfertigt:

#include <stdio.h>
int main(){ unsigned int a=0xC0000000, b=0xA0000000;
printf("%x %x %x %x\n",a,   b,       a|b,       a&b);
printf("%x %x %x %x\n",a+b, a-(a&b), a-(a&b)+b, a+b-(a&b)); }

c0000000 a0000000 e0000000 80000000
60000000 40000000 e0000000 e0000000

bearbeiten : Ich habe das also geschrieben, bevor es Antworten gab, dann gab es eine 2-stündige Unterbrechung meiner Heimverbindung, und ich habe es schließlich geschafft, es zu posten, und habe erst danach bemerkt, dass es bereits zweimal richtig beantwortet wurde. Ich persönlich ziehe es vor, mich auf eine Wahrheitstabelle zu beziehen, um bitweise Operationen auszuarbeiten, also lasse ich es hier, falls es jemandem hilft.

Answer 4