Welche Art von Algorithmus macht eine Kurve wie diese (img) & kann es in javascript für flot getan werden?

Question

Und können Sie mir ein Beispiel für einen Algorithmus nennen? Alt-Text http://ryancalderoni.com/archive/ideal_curve.jpg

EDIT: Und wie würde ich dann die Mathematik mit Javascript berechnen? Kann das jemand ergänzen? Tut mir leid, dass ich diesen Kontext ursprünglich nicht mit einbezogen habe

HINWEIS: Ich verwende "flot", um es grafisch darzustellen, und die Eingabe für flot ist ein Javascript-Array wie dieses:

[[x,y],[x,y],[x,y]...]

Angesichts der Werte, die die Kurve verändern, gebe ich also alle Punkte in einem Array mit einer Schleife aus und spucke sie in einem Diagramm aus.

Answer 1

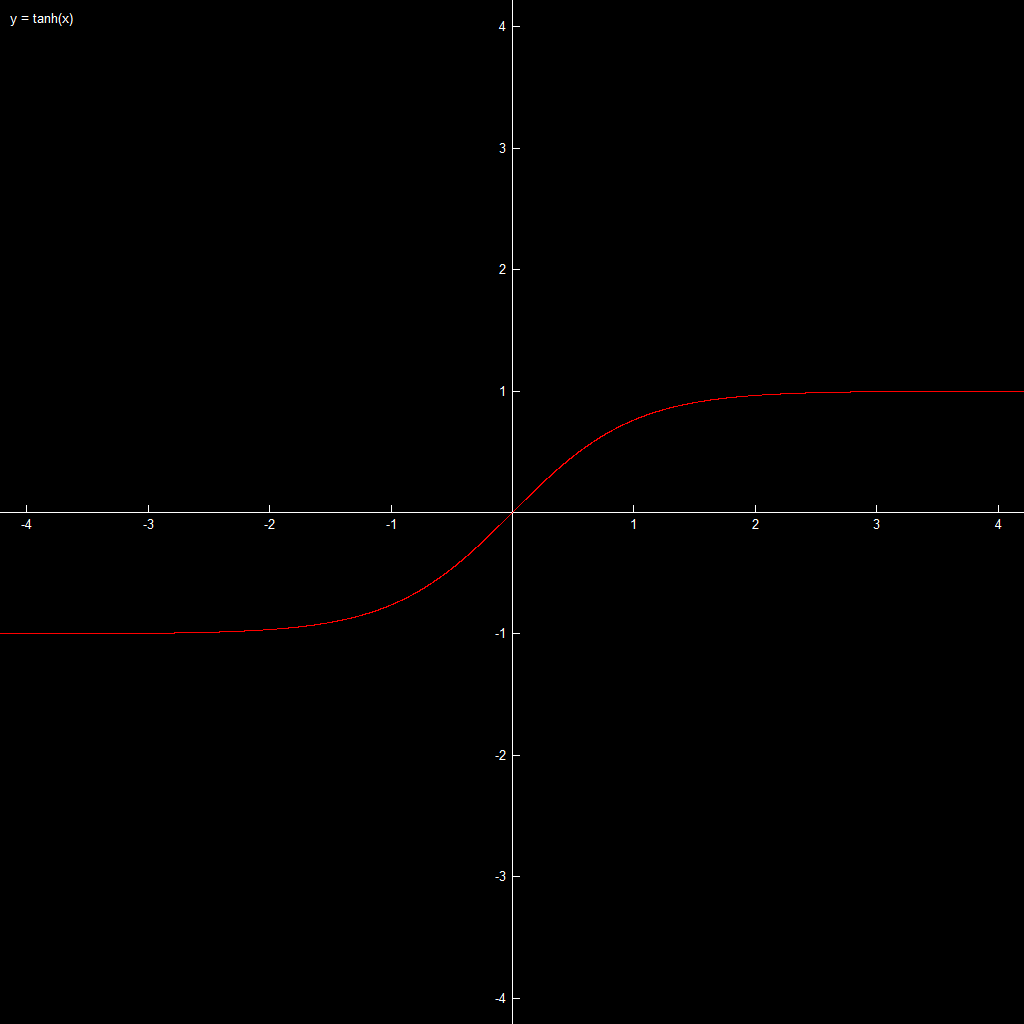
Eine typische sigmoide Kurve ist die tanh(x)-Kurve.

Per Definition,

  tanh(x) = sinh(x) / cosh(x) =
          = [(1/2) (e^x - e^-x)] / [(1/2) (e^x + e^-x)] =
          = (e^x - e^-x) / (e^x + e^-x) = 
          = (e^(2x) - 1) / (e^(2x) + 1)

(Hochauflösend)

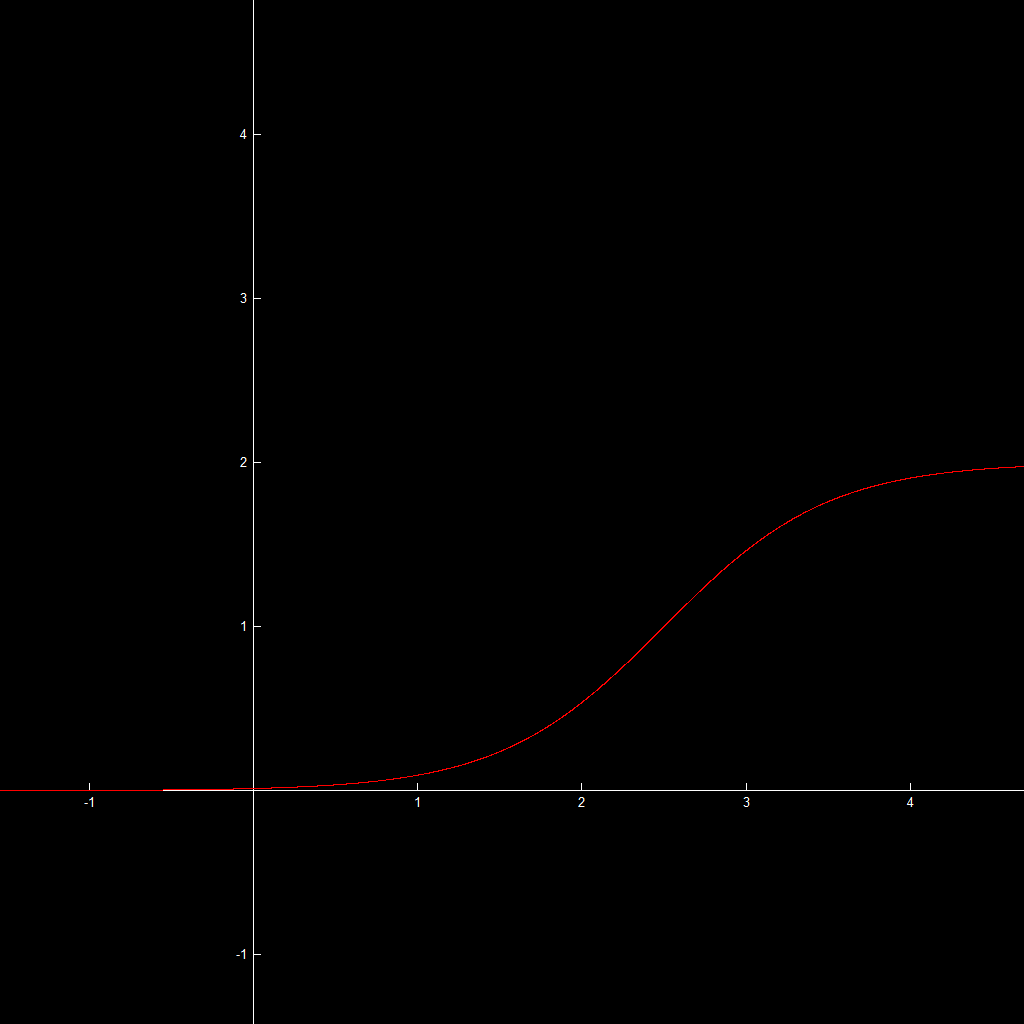
Beachten Sie, dass die Symmetrielinien in Bezug auf Ihr Beispielbild verschoben sind. Damit ein tanh-Diagramm Ihrem Beispiel ähnlicher wird, verschieben Sie es einfach nach oben und nach rechts:

y = 1 + (e^(2x - 6) - 1) / (e^(2x - 6) + 1)

(Hochauflösend)

In JavaScript implementieren Sie diesen Ausdruck am effizientesten als

exp2x = Math.exp(2*x)
y = (exp2x - 1) / (exp2x + 1)

Update (wieder)

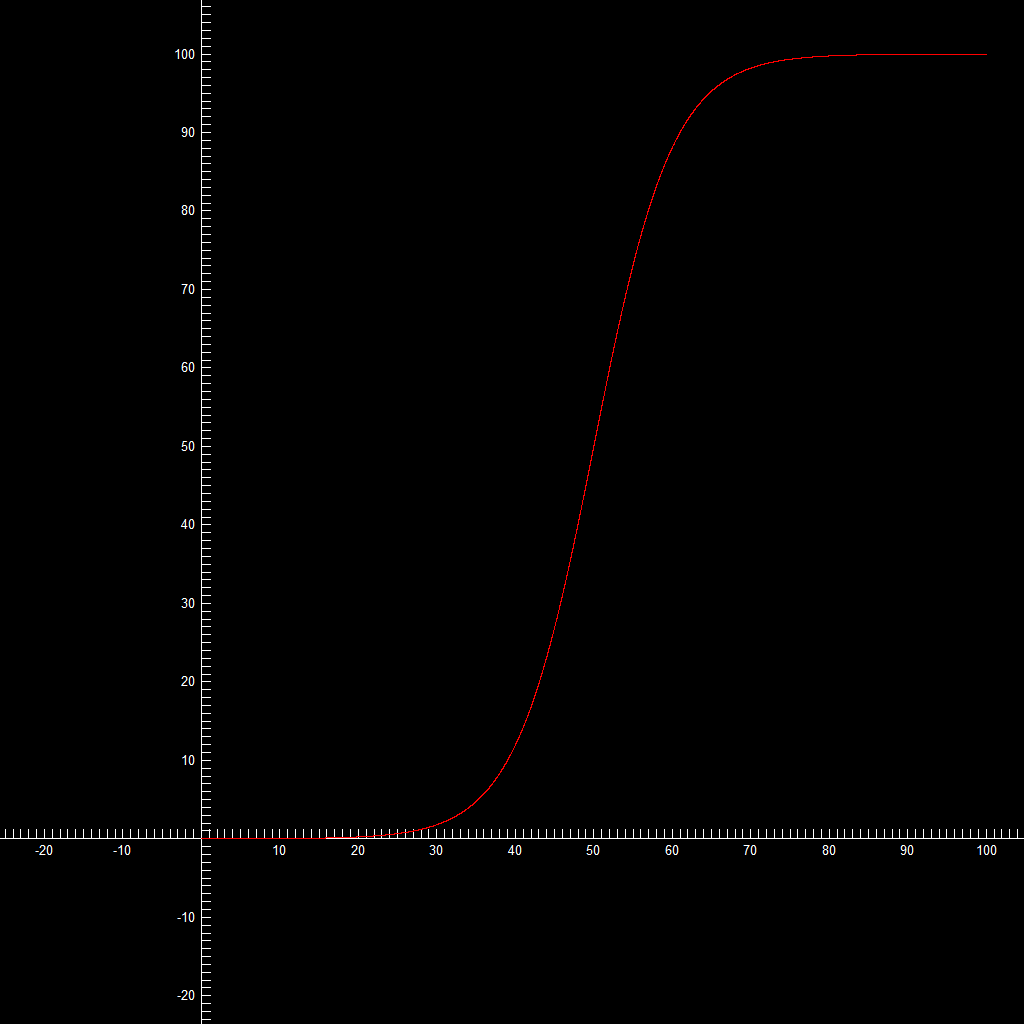
OK, wenn Sie möchten, dass y von 0 bis 100 und x von 0 bis 100 reicht, dann sollten Sie versuchen

y = 50 + 50*tanh((x50)/10)

die wie folgt aussieht

(Hochauflösend)

Ahora

y = 50 + 50 * tanh((x50)/10)
  = 50 + 50 * (e^((x50)/5) - 1) / (e^((x50)/5) + 1)

Die Fehlerfunktion erf sieht ganz ähnlich aus, ist aber viel schwieriger zu berechnen (es sei denn, JavaScript hat eine eingebaute erf-Funktion).

---

Ryan (OP) fügt hinzu: umgesetzt!

var y = 50 + 50 * tanh((n-50)/10);

function tanh (arg) {
    return (Math.exp(arg) - Math.exp(-arg)) / (Math.exp(arg) + Math.exp(-arg));
}

Answer 2

Wenn Sie eine einzelne, analytische Funktion wünschen, dann haben ArcTangent und Hyperbolic Tangent beide diese Form, Sie müssen sie nur ein wenig verschieben. Wenn Sie wollen, dass die Kurve nur am Ursprung beginnt und flach ist, sehen Sie sich Exp[-1/x^n] für n>=1 an. Dies ergibt eine Kurve, die im Ursprung sehr flach ist.

Answer 3

Versuchen Sie, die Sigmoidfunktion nachzuschlagen, sie sieht ihr sehr ähnlich.

_{(Quelle: <a href="http://ulcar.uml.edu/~iag/CS/Sigmoid-function.GIF" rel="nofollow noreferrer">iag at ulcar.uml.edu </a>)}

Answer 4

A Bézier-Kurve ? Der entsprechende Algorithmus zum Zeichnen würde lauten de Casteljau's Algorithmus .

Answer 5

Darf ich vorschlagen:

• Die Fehlerfunktion ( erf(x) in C)
• Die kumulative Normalverteilungsfunktion ( 0.5 * erfc(-x/sqrt(2)) )
• Die logistische Funktion ( 1.0 / (1.0 + exp(-x)) )
• Jede andere sigmoide Funktion