http://en.wikipedia.org/wiki/Fibonacci_number
Fibonacci selbst begann die Folge mit 1 und nicht mit 0. Es ist wichtig zu erkennen, dass die eigene Meinung keine unumstößliche Tatsache ist, und es kann sich lohnen, zu bedenken, dass man es nicht unbedingt besser weiß als der Mann, der die Folge geschaffen hat. Ich denke, es ist in Ordnung, die Sequenz mit 0 zu beginnen, solange man nicht so tut, als sei das die einzig absolut richtige Vorgehensweise, denn die Zahl bei "Index 0" ist grundsätzlich mehrdeutig und sollte immer explizit kommuniziert werden.
Die Frage des "Index" gilt nur für uns und nicht für Fibonacci. Wenn wir also mit seiner Startnummer beginnen wollen und wir 0-basierte Indizes verwenden, würden wir seine Startnummer bei Index 0 setzen, oder wenn wir 1-basierte Indizes verwenden, würden wir seine Startnummer bei Index 1 setzen.
Und da es in der Tat möglich ist, die Folge nach links fortzusetzen, ist es auch völlig willkürlich, mit 0 zu beginnen. Warum nicht mit -1 beginnen und dann -1, 1, 0, 1, 1, 2...?


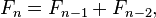
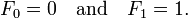


7 Stimmen
Fib 0 = 0 ist richtig. Aber für manche Menschen ist die Erde flach und Fib 0 = 1.
0 Stimmen
Steht dies im Zusammenhang mit dem Projekt euler?
1 Stimmen
In Anbetracht der Tatsache, dass jeder von uns die Wikipedia-Seite ändern kann, würde ich mich an die Definition aus der Encylopedia Britannica halten: britannica.com/wissenschaft/Fibonacci-Zahlen Fib beginnt mit 1, wie von Fibonacci selbst definiert.
1 Stimmen
Wollten Sie sagen
Program with fib(0) = 0; spits out fib(4) = 3?